6.892 Algorithmic Lower Bounds: Fun with Hardness Proofs (Spring 2019)

Prof. Erik Demaine TAs: Jeffrey Bosboom, Jayson Lynch

[Home] [Lectures] [Problem Sets] [Project] [Coauthor] [Accessibility]

Lecture 9 Video [previous] [next] [completion form]

[+] Graph Problems.
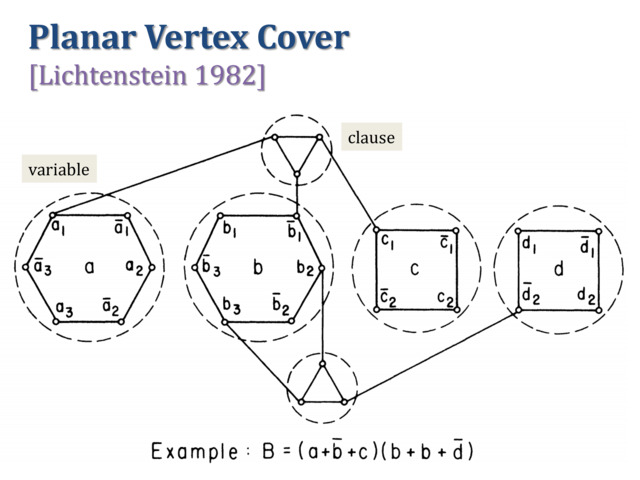
Vertex Cover: planar max-degree-3; exact vertex cover (polynomial), edge cover (polynomial), connected vertex cover, rectilinear Steiner tree.
Vertex Coloring: planar max-degree-4 3-coloring, max-degree-3 3-coloring (polynomial), Push-1X, Push-1G (gravity).
Graph Orientation: 1-in-3, 2-in-3, 0-or-3 vertices; packing trominoes.
Graph Layout: Bandwidth, minimum linear arrangement, cutwidth, vertex separation, sum cut, edge bisection, vertex bisection; betweenness; bipartite crossing number, crossing number, Rubik's Cube.

This lecture is our last about straight-up NP-hardness. We've already seen the main techniques for such proofs, but there are a few other techniques that get used now and then. We will see three:

Vertex cover, in particular planar vertex cover and planar connected vertex cover
Vertex coloring, in particular planar max-degree-4 3-coloring
Graph orientation, about assigning edge directions to satisfy vertex constraints.

In particular, we will use these techniques to prove hardness of

Rectilinear Steiner tree
Pushing-block puzzles Push-1X and Push-1G (gravity)
Crossing number
A version of Rubik's Cube (just a rough sketch)

In this class, we'll tackle several problems related to #P/ASP and PSPACE-complete one-player games. We'll also cover the corresponding unbounded one-player general theory of gadgets, as well as a little bit about the Polynomial Hierarchy (Σ_k and Π_k, between NP and PSPACE).