|
[+]
SAT Reductions. Nintendo games (Super Mario World, glitches, Legend of Zelda,
Metroid, Donkey Kong Country, Pokémon); Conway's Phutball
(Philosopher's Football), mate-in-1, Checkers; cryptarithms
(alphametics); origami flat-foldable crease patterns;
vertex-disjoint paths (Numberlink) |
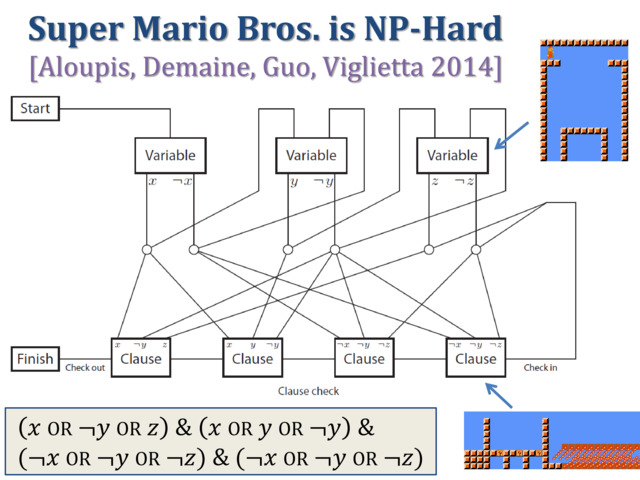
In this class, we'll talk about a new level of planar 3SAT called
linked planar 3SAT. This problem is motivated by the type of
planarity needed in e.g. the Super Mario Bros. NP-hardness proof:
- visit all the variables in some order to make choices,
- affect all the incident clauses, and then
- visit all the clauses in some order to check that they're all satisfied.
Surprisingly, 3SAT remains NP-hard with this level of planarity, thanks to
a paper by Pilz in 2018.
Unfortunately, reducing from this problem is not quite
as easy as it seems, as we need to take care about which sides the
connections are on at the clause.
We'll also have many solved and open problems related to planar SAT and
circuit SAT and their many variations.
Finally, we'll plan a bit for what to do with all the solutions to open
problems we've been coming up with: research papers, final projects, etc.
|