[+] Rigidity theory: Rigidity, generic rigidity, minimal generic rigidity, Henneberg characterization, Laman characterization, polynomial-time algorithm, convex polyhedra. |
|||
|
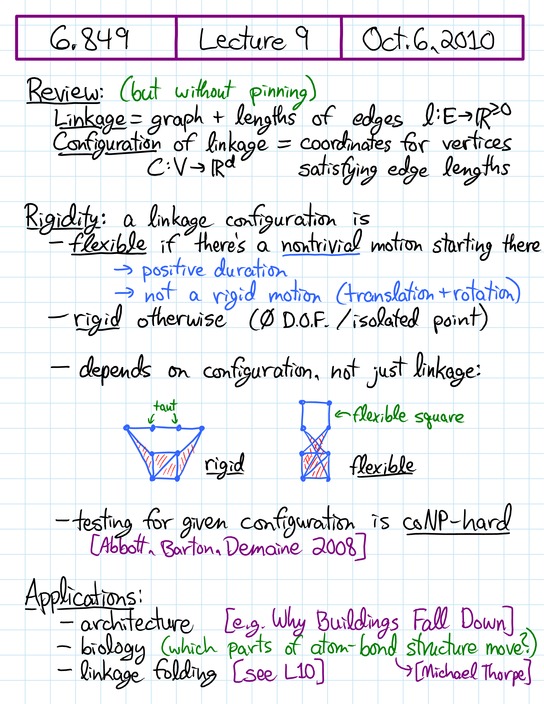
This lecture is about rigidity theory, which is about telling
when a linkage can fold at all. This field goes back to mechanical
engineering of the 18th and 19th centuries, with applications to
structural engineering and architecture (getting buildings and
bridges to stand up), biology (understanding which parts of a protein
still move after folding up), and linkage folding itself (beyond just
“does it move at all?”, as we'll see in the next lecture).
We'll cover two main theorems characterizing “generically” rigid graphs in 2D. Henneberg's Theorem, from 1911, gives a nice and direct characterization, but it's hard to turn into an algorithm. Laman's Theorem, from 1970, is intuitively harder to work with, but turns into a fast (quadratic-time) algorithm. Unfortunately, this is all just for 2D, and we don't know any good characterizations for generic rigidity in 3D. I'll briefly describe some nice theorems about the rigidity of convex polyhedra in 3D, though, which in particular explain why Buckminster Fuller's geodesic domes stand up. |
|
Handwritten notes, page 1/10 •
[previous page] •
[next page] •
[PDF]
Handwritten notes, page 1/10 • [previous page] • [next page] • [PDF] |
|
|
Slides, page 1/6 •
[previous page] •
[next page] •
[PDF]
http://www.flickr.com/photos/21953562@N07/4050394485/ Licensed under Creative Commons Attribution-NonCommercial 2.0 license. Slides, page 1/6 • [previous page] • [next page] • [PDF] |
The video above should play if your web browser supports either modern Flash or HTML5 video with H.264 or WebM codec. The handwritten notes and slides should advance automatically. If you have any trouble with playback, email Erik.
