[+]
Folding motions: folded states vs. motions;
universal foldability of polygonal paper. |
|||
|
This lecture kicks off the beginning of linkage folding.
We'll segue from origami by thinking about folding motions of pieces of
paper, and prove that it's always possible to reach any folded state
of a polygonal piece of paper. How many extra creases do we need?
This unsolved question leads to problems in the linkage-folding domain.
Then we'll focus on Kempe's Universality Theorem: there's a linkage to sign your name, or more mathematically, trace any polynomial curve. This proof introduces a bunch of cool gadgets, in particular to add angles and multiply (or divide) angles by constant factors. |
|
Handwritten notes, page 1/9 •
[previous page] •
[next page] •
[PDF]
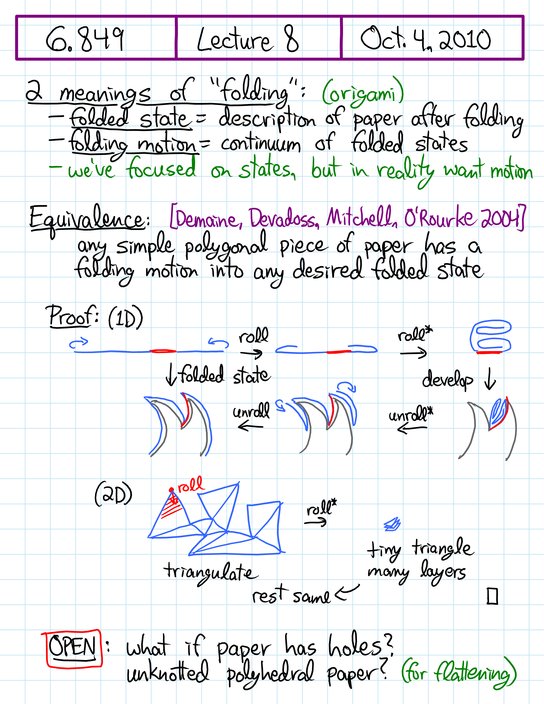
Handwritten notes, page 1/9 • [previous page] • [next page] • [PDF] |
|
|
Slides, page 1/13 •
[previous page] •
[next page] •
[PDF]
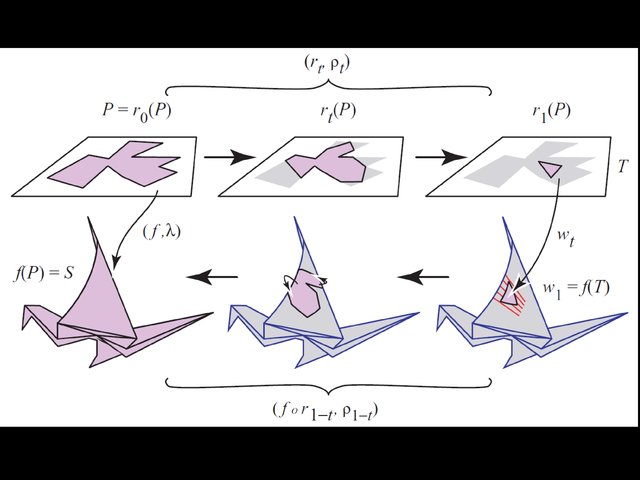
Figure 11.13 of GFALOP Slides, page 1/13 • [previous page] • [next page] • [PDF] |
The video above should play if your web browser supports either modern Flash or HTML5 video with H.264 or WebM codec. The handwritten notes and slides should advance automatically. If you have any trouble with playback, email Erik.
