Handwritten notes, page 1/7 •
[previous page] •
[next page] •
[PDF]
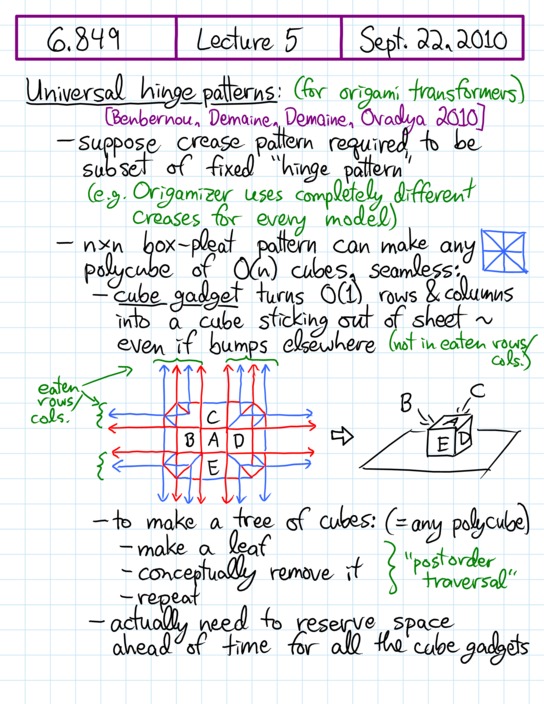
Handwritten notes, page 1/7 • [previous page] • [next page] • [PDF]
Slides, page 1/20 •
[previous page] •
[next page] •
[PDF]

http://www.pnas.org/content/107/28/12441 / http://www.pnas.org/content/suppl/2010/06/25/0914069107.DCSupplemental / http://erikdemaine.org/papers/Matter_PNAS/ (covered under the MIT Faculty Open-Access Policy)
Slides, page 1/20 • [previous page] • [next page] • [PDF]