6.849: Geometric Folding Algorithms: Linkages, Origami, Polyhedra (Fall 2012)

Prof. Erik Demaine       TA: Jayson Lynch

[Home] [Problem Sets] [Project] [Lectures] [Problem Session Notes] [Accessibility]

Class 7 Video     [previous] [next]

[+] Universal hinge patterns: box-pleating history; maze-folding prints.
NP-hardness: simple foldability; crease pattern flat foldability.
This class starts with some artistic examples related to the two universality results covered in Lecture 7: box pleating and maze folding.

Second, we review the NP-hardness proofs from Lecture 7:

  • What does hardness really mean?
  • Details of the simple fold hardness proof
  • Details of the flat foldability hardness proof
  • Extension to when given the mountain-valley assignment

Finally, we cover a new (this year) result: 2 × n map folding can be solved in polynomial time. (m × n map folding remains unsolved.)

Download Video: 360p, 720p

Handwritten notes, page 1/5 • [previous page] • [next page] • [PDF]

Handwritten notes, page 1/5 • [previous page] • [next page] • [PDF]

Slides, page 1/32 • [previous page] • [next page] • [PDF]

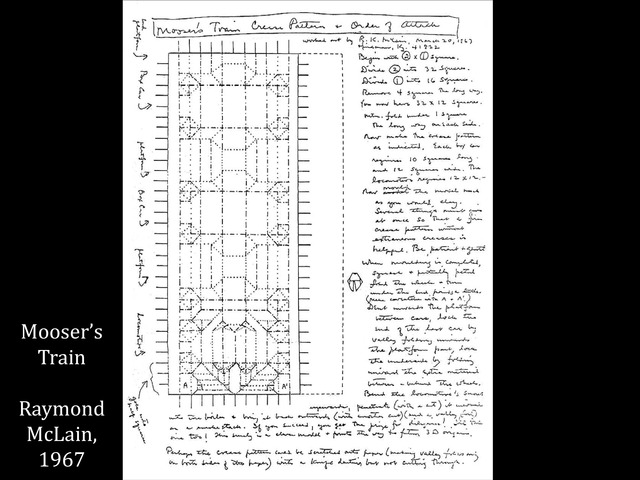
Figure 12.4 on page 423 of Origami Design Secrets (1st edition)

Slides, page 1/32 • [previous page] • [next page] • [PDF]

The video above should play if your web browser supports either modern Flash or HTML5 video with H.264 or WebM codec. The handwritten notes and slides should advance automatically. If you have any trouble with playback, email Erik.