|
This lecture is all about efficient origami design.
We saw in Lecture 2 how to fold anything impractically.
Now we'll see how to fold many shapes practically.
First up is the tree method, whose software implementation TreeMaker
I demoed at the end of Lecture 3. I'll describe how it lets us
fold an optimum stick-figure (tree) origami base, although computing
that optimum is actually NP-complete (as we'll see in Lecture 5).
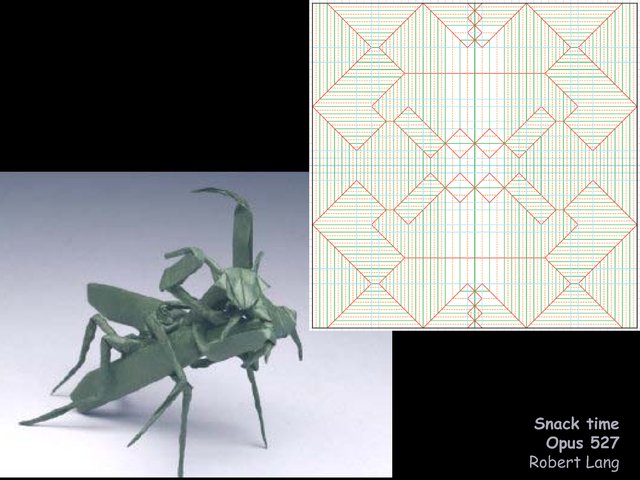
This algorithm is used throughout modern complex origami design;
I'll show some examples by Robert Lang and our own Jason Ku.
Second we'll look at a simple, fully understood case:
the smallest square to fold a cube.
Third we'll look at a classic problem that we made progress on recently:
folding an n × n checkerboard from the
smallest bicolor square.
Finally we'll look at the latest and most general method, Origamizer,
for folding any polyhedron reasonably efficiently. Here we don't have
a nice theoretical guarantee on optimality, but the method works well
in practice, provably always works, and has other nice features such as
watertightness.
|