6.849: Geometric Folding Algorithms: Linkages, Origami, Polyhedra (Fall 2010)
[Home]
[Problem Sets]
[Project]
[Lectures]
[Problem Session Notes]
[Accessibility]
Overview
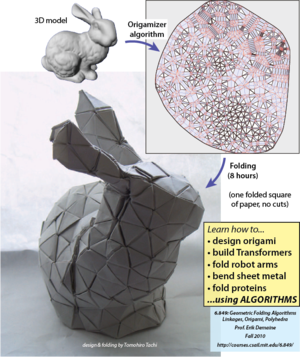
the algorithms behind building TRANSFORMERS and designing ORIGAMI
Whenever you have a physical object to be reconfigured, geometric folding
often comes into play. This class is about algorithms for analyzing and
designing such folds. Motivating applications include
Major progress have been made in recent years in many of these directions,
thanks to a growing understanding of the mathematics and algorithms
underlying folding. Nonetheless, many fundamental questions remain
tantalizingly unsolved. This class covers the state-of-the-art in folding
research, including a variety of open problems, enabling the student to do
research and advance the field.
We will organize an optional problem-solving session, during which we can
jointly try to solve open problems in folding. In the past, these sessions
have led to important new results and published papers, as well as class
projects.
Class projects more generally can take the form of
folding-inspired sculptures; formulations of clean, new open problems;
implementations of existing algorithms; or well-written descriptions of one or
more papers in the area. Projects can be purely mathematical (geometric)
and/or theoretical computer science (algorithmic/complexity theoretic) and/or
artistic. Students are also required to do a project presentation and a
small number of problem sets.
Topics
This is an advanced class on computational geometry focusing on folding and
unfolding of geometric structures including linkages, proteins, paper, and
polyhedra. Examples of problems considered in this field:
- What forms of origami can be designed automatically by algorithms?
- What shapes can result by folding a piece of paper flat and
making one complete straight cut?
- What polyhedra can be cut along their surface and unfolded into a flat
piece of paper without overlap?
- When can a linkage of rigid bars be untangled or folded into a
desired configuration?
Many folding problems have applications in areas including manufacturing,
robotics, graphics, and protein folding. This class covers many of the results
that have been proved in the past few years, as well as the several exciting
open problems that remain open.
Textbook
The textbook for the class is
Geometric Folding Algorithms:
Linkages, Origami, Polyhedra
by Erik Demaine and
Joseph O'Rourke,
published by Cambridge University Press (2007).
The list price for the hardback is $99.
Nine copies will be available at the MIT Coop at this price.
Amazon
offers a sale price of $79.
A further reduced price is available as part of a bulk class purchase;
let Erik know if you want to be part of it.
Additional recommended reading is
Origami Design
Secrets: Mathematical Methods for an Ancient Art
by Robert Lang.
Specifics
| Lecture Time: |
Mondays and Wednesdays at 11:00am–12:30pm |
| Lecture Room: |
MIT room
4-163
|
| First Lecture: |
Wednesday, September 8, 2010 |
| Problem Session Time: |
Mondays at 5:00pm-7:00pm |
| Problem Session Room: |
36-153 |
| Professor: |
Erik Demaine,
32-G680 |
| Units: |
3-0-9 |
| Prerequisites: |
6.046 or equivalent background in discrete mathematics and algorithms
Alternatively, permission from the instructor.
|
| Credit: |
H-level and EC-level credit; no ED credit |
| Requirements: |
Written project and project presentation.
Small number of problem sets. |
Participating
We welcome both undergraduate and graduate students from all universities,
although officially this is a graduate class.
If you are interested in attending the class, for credit or as a listener,
please join the
6849-students mailing list.
Previous Offerings
This class was offered twice before under the class number 6.885,
in Fall 2007 and Fall 2004.
You might be interested in the lecture notes, problem sets, etc.
from those offerings.