Handwritten notes, page 1/8 •
[previous page] •
[next page] •
[PDF]

Handwritten notes, page 1/8 • [previous page] • [next page] • [PDF]
Slides, page 1/26 •
[previous page] •
[next page] •
[PDF]
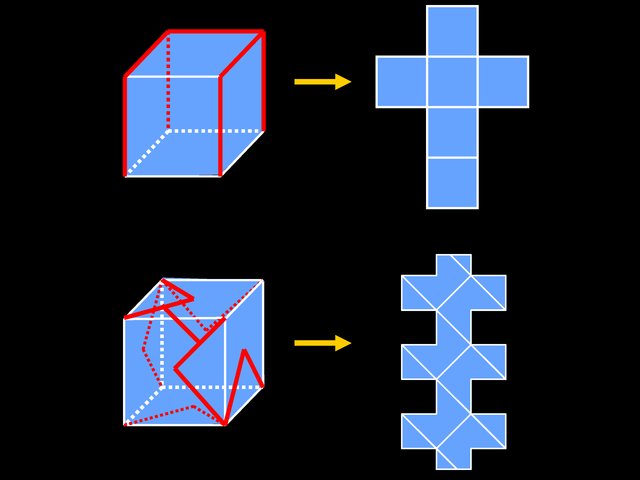
Edge unfolding vs. general unfolding (figures drawn by Erik Demaine)
Slides, page 1/26 • [previous page] • [next page] • [PDF]