6.5310: Geometric Folding Algorithms: Linkages, Origami, Polyhedra (Spring 2025)

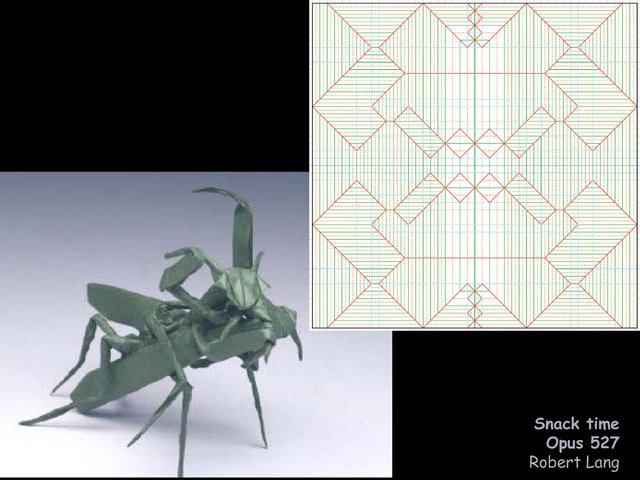
First up is the tree method, whose software implementation TreeMaker I demoed at the end of Lecture 2. I'll describe how it lets us fold an optimum stick-figure (tree) origami base, although computing that optimum is actually NP-complete (as we'll see in Lecture 6). This algorithm is used throughout modern complex origami design; I'll show some examples by Robert Lang and our own Jason Ku.

Second we'll look at a simple, fully understood case: the smallest square to fold a cube.

Third we'll look at a classic problem that we made progress on recently: folding an n × n checkerboard from the smallest bicolor square.

Finally we'll look at the latest and most general method, Origamizer, for folding any polyhedron reasonably efficiently. Here we don't have a nice theoretical guarantee on optimality, but the method works well in practice, provably always works, and has other nice features such as watertightness.