
textbook
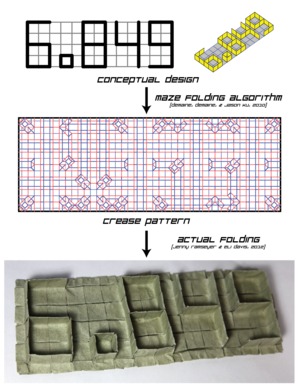
old poster
(see Origami Maze Folder
and associated paper)
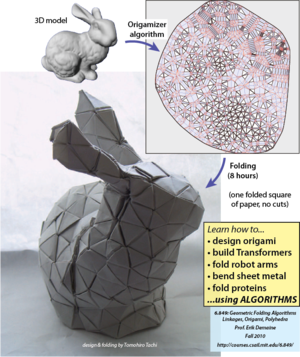
older poster
(see Origamizer
and bunny video)


old poster
(see Origami Maze Folder
and associated paper)

older poster
(see Origamizer
and bunny video)
the algorithms behind building TRANSFORMERS and designing ORIGAMI
Whenever you have a physical object to be reconfigured, geometric folding often comes into play. This class is about algorithms for analyzing and designing such folds. Motivating applications includeThis class features inverted lectures: most material is covered in video lectures recorded in 2010 and 2012 (already watched by over 30,000 people), which you can conveniently play at faster speed than real time. In-class time will be focused on collaborative problem solving with your fellow students and the course staff. Particularly unusual is that the problems we'll solve in groups will include a choose-your-own-mix of problem-set style problems with known solutions, design problems for those who love to create, coding problems for those who love programming, and open research problems that no one knows the answer to, with the goal of publishing papers about whatever we discover. (Past offerings of this class have led to over a dozen published papers.) You can work on whatever type of problem most interests you. To facilitate collaboration, we'll be using our open-source software platform called Coauthor, along with GitHub for (optional) coding.
Additional recommended reading:
| Class Time: | Tuesdays and Thursdays at 11:00am–12:30pm
(or until 1pm for those who want to stick around) |
|---|---|
| Class Room: | MIT room 32-082 |
| First Class: | Tuesday, February 4, 2025 |
| Office Hours: | Tuesdays and Thursday at 12:30pm–1pm |
| Professor: | Erik Demaine, edemaine at mit.edu |
| TAs: | Josh Brunner, brunnerj at mit.edu
Jenny Diomidova, diomidova at mit.edu |
| Design Advisor: | Alfonso Parra Rubio, aprubio at mit.edu |
| Staff Email: | 65310-staff at csail.mit.edu |
| Units: | 3-0-9 |
| Prerequisites: | 6.1220 or equivalent background in discrete mathematics and algorithms.
Alternatively, permission from the instructor. |
| Credit: | EECS, AAGS (Theoretical CS Concentration) |
If you are interested in attending the class, for credit or as a listener, please do the following:
| required | Watch all video lectures, measured by thumbs-upping completion questions on Coauthor (see your stats). |
| required | Participate during all (or most) in-person classes (email 65310-staff about exceptions) |
| required |
Participate in class discussion,
measured as coauthoring at least one nontrivial Coauthor post each week.
See your
statistics view to check for zero weeks.
(Example of a trivial post for a solved problem: "Apply methods from lecture." Example of a nontrivial post for a solved problem: Describing the solution techniques you tried but failed. Deleted and unpublished posts do not count, but private posts do.) |
| choice | Problem sets. Problem sets will be posted weekly. |
| choice | Project write-up and presentation based on in-class work. |
We're experimenting with a flexible grading scheme this semester:
The percentage weights sum to more than 100%. To compute your overall grade, we will reduce the percentage weight on your lowest-scoring problem set or project (whose weight isn't already zero) until the total weight reaches 100%. This lets you make up for lost points in one component by working more on the other components. In particular, three reasonable approaches to taking this class are to do problem sets and no project (20% + 40% + 50% = 110%, so still plenty of room to make up mistakes); one normal project and no problem sets (also 110%); or one small project and half the problem sets (also 110%). You can also do any combination, including multiple projects.
One additional rule is that you cannot pass the class without both watching most of the lectures and in-class participation most weeks (according to the fairly minimal requirements above), which is the meaning of "required".
Each component will be graded on a 100-point scale, then weighted as described above, then summed to produce your overall score. Your letter grade (A, B, etc.) will be assigned according to this score (where 90+ = A, 80+ = B, 70+ = C, 60+ = D, <60 = F). However, we reserve flexibility in assigning the annotation (+, −, or straight letter) according to other factors such as going above and beyond in participation or just scraping by.