|
[+]
Parameterized Complexity II: ETH & Planar.
Exponential Time Hypothesis (ETH), strong ETH,
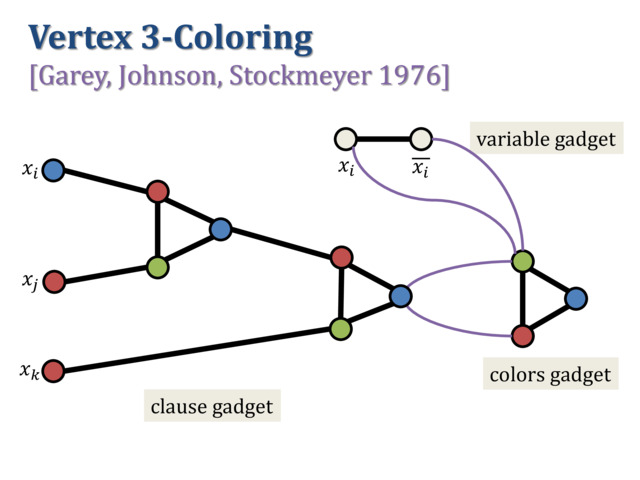
3-coloring, reduction size blowup, vertex cover, dominating set,
Hamiltonicity, independent set, clique, planar 3SAT,
planar graph problems, parameterized consequences of ETH,
parameter blowup.
Planar problems: Grid Tiling, list coloring, grid tiling with ≤,
scattered set, independent set in unit-disk graphs.
|
|
This lecture is about strong lower bounds on running time that
are possible by assuming the Exponential Time Hypothesis: there is no
2o(n)
algorithm to solve n-variable 3SAT. This conjecture is a stronger form of
P ≠ NP, and it lets us keep track of “problem size blow-up”, something we've
ignored before in our NP-hardness reductions. Many of the reductions we've
seen, such as 3-coloring, vertex cover, dominating set, Hamiltonicity, and
Independent Set/Clique have linear blow-up, so we get
2o(n) lower bounds.
On the other hand, planar versions of these problems (except Clique)
have quadratic blow up because of the crossover gadgets, so we get
2o(√n) lower bounds.
In parameterized complexity, we get a particularly strong form of FPT ≠ W[1]:
there is no f(k) no(k)
algorithm for Clique/Independent Set, for any
computable function f. In particular, there's no
f(k) nO(1) (FPT) algorithm.
By keeping track of the parameter blowup in our parameterized reductions,
we can prove similar bounds for other problems, e.g. multicolored
Clique/Independent Set, Dominating Set, Set Cover, and Partial Vertex Cover.
Finally, we'll cover a useful base problem, called Grid Tiling, for proving
W[1]-hardness of problems on planar graphs or in 2D. Specifically, we'll
use Grid Tiling to prove Scattered Set is W[1]-hard in planar graphs,
and that Independent Set is W[1]-hard in in unit-disk graphs.
These results also imply that these problems have no EPTAS.
|