| [+] Planar SAT. Planar 3SAT, planar monotone rectilinear 3SAT, planar positive 1-in-3SAT, planar NAE 3SAT (polynomial!), planar X3C, planar 3DM; planar vertex cover, planar (directed) Hamiltonian cycle, Shakashaka, flattening fixed-angle chains | |||||
|
This lecture introduces planar versions of 3SAT, in particular planar monotone rectilinear 3SAT and planar positive rectilinear 1-in-3SAT. But be careful: planar NAE 3SAT is polynomial. We will prove these versions of planar SAT are NP-hard. Then we'll reduce them to problems on planar graphs and in 2D geometry:
| |||||
|
Handwritten notes, page 1/5 •
[previous page] •
[next page] •
[PDF]
Handwritten notes, page 1/5 • [previous page] • [next page] • [PDF] |
|
|
Slides, page 1/37 •
[previous page] •
[next page] •
[PDF]
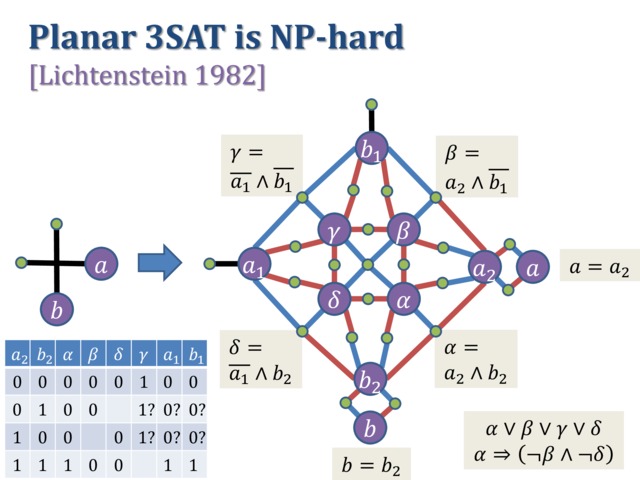
Figure drawn by Erik Demaine based on Figure 4 of http://dx.doi.org/10.1137/0211025 Slides, page 1/37 • [previous page] • [next page] • [PDF] |
