Lecture notes, page 1/13 •
[previous page] •
[next page] •
[PDF]
Lecture notes, page 1/13 • [previous page] • [next page] • [PDF]
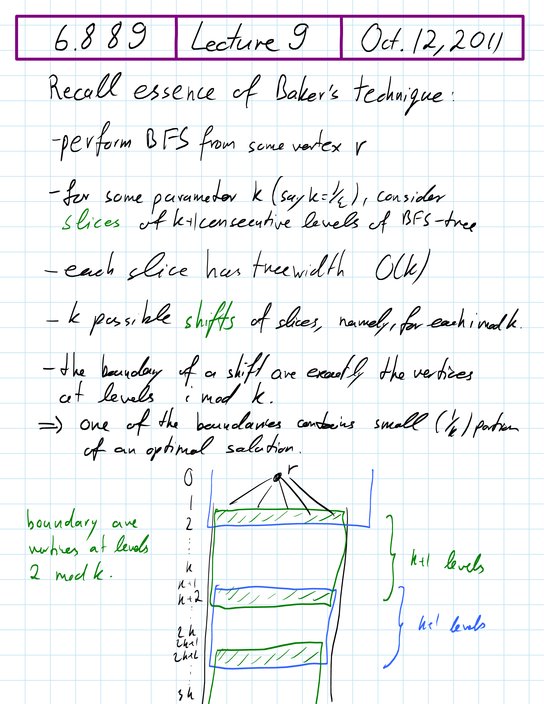
[+] Approximation schemes in minor-free graphs I: local treewidth and apex-minor-free graphs, extension to H-minor-free graphs, deletion decomposition |
| In this
lecture we look at Baker's technique from another perspective which
leads to the notion of deletion decomposition: partitioning a graph
into k parts such that removing any part gives a graph of low
treewidth (in k). This idea of a simplifying decomposition is one of
the main themes of this course.
We will then see how to generalize this idea from planar graphs to apex-minor-free graphs. To this end, we introduce the notion of local treewidth, one of the major concepts in algorithmic graph structure theory. For the generalization to H-minor-free graphs we will have to look at the Robertson-Seymour decomposition of H-minor-free graphs into clique-sums of almost embeddable graphs. All in all, we obtain a clean and simple deletion decomposition theorem for all H-minor-free graphs that can be used to obtain many approximation algorithms, PTASes, and parameterized algorithms. |
|
Lecture notes, page 1/13 •
[previous page] •
[next page] •
[PDF]
Lecture notes, page 1/13 • [previous page] • [next page] • [PDF] |
|
The video above should play if your web browser supports either modern Flash or HTML5 video with H.264 or WebM codec. The lecture notes should advance automatically. If you have any trouble with playback, email Erik.