Handwritten notes, page 1/9 •
[previous page] •
[next page] •
[PDF]
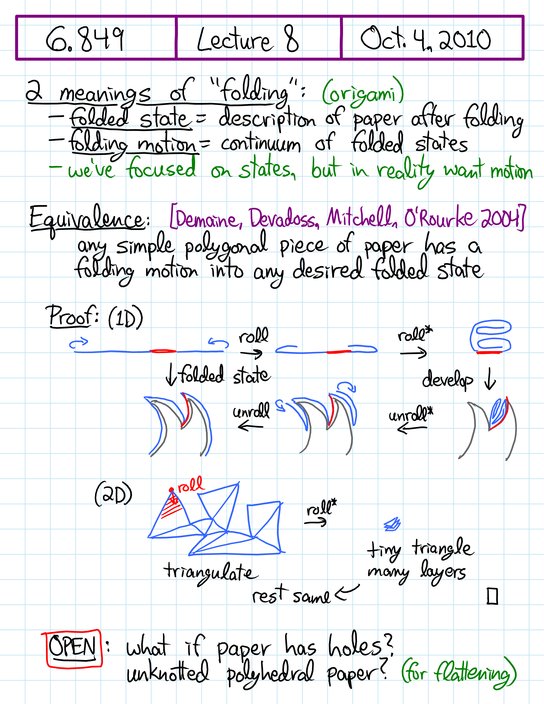
Handwritten notes, page 1/9 • [previous page] • [next page] • [PDF]
Slides, page 1/13 •
[previous page] •
[next page] •
[PDF]
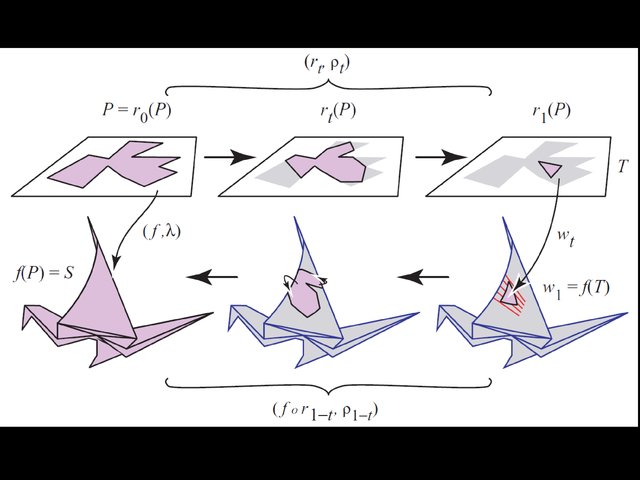
Figure 11.13 of GFALOP
Slides, page 1/13 • [previous page] • [next page] • [PDF]