
textbook
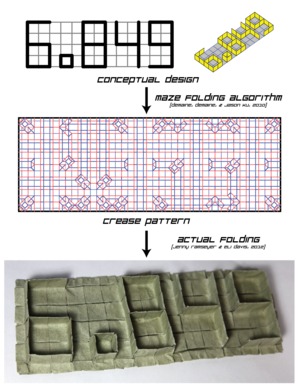
poster
(see Origami Maze Folder
and associated paper)
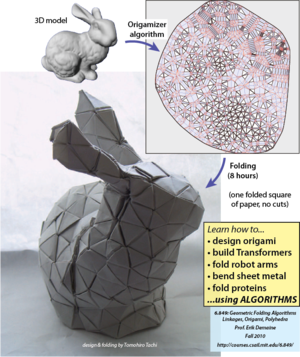
old poster
(see Origamizer
and bunny video)


poster
(see Origami Maze Folder
and associated paper)

old poster
(see Origamizer
and bunny video)
the algorithms behind building TRANSFORMERS and designing ORIGAMI
Whenever you have a physical object to be reconfigured, geometric folding often comes into play. This class is about algorithms for analyzing and designing such folds. Motivating applications includeMost course material is covered in video lectures recorded in 2010 (already watched by over 19,000 people), which you can conveniently play at faster speed than real time. There may also be some new material presented by the professor and/or guest lecturers, which will be recorded for asynchronous viewing.
But synchronous meeting time (also online) will focus on collaborative problem solving with your fellow students and the course staff. Particularly unusual is that the problems we'll solve in groups will include a choose-your-own-mix of problem-set style problems with known solutions, design problems for those who love to create, coding problems for those who love programming, and open research problems that no one knows the answer to, with the goal of publishing papers about whatever we discover. (Past offerings of this class have led to over a dozen published papers.) You can work on whatever type of problem most interests you. To facilitate collaboration, we'll be using our open-source software platform called Coauthor, along with GitHub for (optional) coding.
We recommend a drawing tablet for online collaboration, so be sure to apply for one if you don't have one. We'll be using a bunch of custom bleeding-edge open-source software tools for online collaboration, including our own Coauthor, Cocreate, and Comingle, which aim to reproduce the in-person experience as best as possible. Join us to help make this possible!
Additional recommended reading:
| Synchronous Class Time: | Mondays at 4:00pm–5:30pm Eastern and/or Thursdays at 7:00–8:30pm Eastern (For-credit students must attend at least one. You are encouraged to attend both if possible.) |
|---|---|
| Synchronous Class Room: | online, using custom software (Fill out the sign-up form and join the mailing list (see below) to get the link to the class.) |
| First Class: | Thursday, September 3, 2020 at 7:00–8:30pm Eastern |
| Second Class: | Tuesday, September 8, 2020 at 4:00–5:30pm Eastern |
| Office Hours: | Monday evenings 10:00—11:00pm Eastern Thursday mornings 10:00—11:00am Eastern |
| Professor: | Erik Demaine, edemaine at mit.edu |
| Co-lecturer: | Martin Demaine, mdemaine at mit.edu |
| TAs: | Jenny Diomidova, diomidova at mit.edu
Klara Mundilova, kmundil at mit.edu |
| Staff Email: | 6849-staff at csail.mit.edu |
| Units: | 3-0-9 |
| Prerequisites: | 6.046 or equivalent background in discrete mathematics and algorithms.
Alternatively, permission from the instructor. |
| Credit: | H-level and TCS AAGS credit |
| Requirements: |
• Watch all video lectures, measured by filling out Completion Forms. • Watch recorded portions of synchronous classes that you didn't attend. • Participation in synchronous classes, at least one per week (email 6849-staff about exceptions). • Participation in discussion, measured as posting or being @mentioned in at least one Coauthor post each week. • Project write-up and presentation. • Problem sets roughly weekly. |
| Grading scheme: | The approximate breakdown of your grade is 50% project, 20% project presentation, 15% psets, and 15% participation. But you cannot pass the class without participating (according to the fairly minimal requirements above). |
If you are interested in attending the class, for credit or as a listener, please do the following: