
textbook
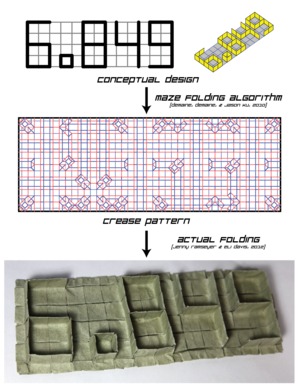
poster
(see Origami Maze Folder
and associated paper)
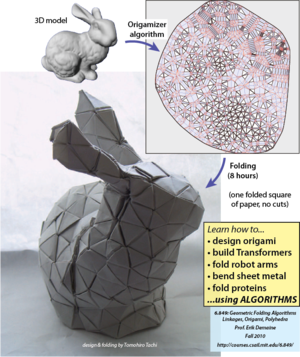
old poster
(see Origamizer
and bunny video)


poster
(see Origami Maze Folder
and associated paper)

old poster
(see Origamizer
and bunny video)
the algorithms behind building TRANSFORMERS and designing ORIGAMI
Whenever you have a physical object to be reconfigured, geometric folding often comes into play. This class is about algorithms for analyzing and designing such folds. Motivating applications includeThis year we will be experimenting with online lectures. Students will be expected to watch recorded lectures, and ask any questions they have via an online form. In-class time will be divided between answers to questions, new material presented by the professor and/or guest lecturers, and in-class problem solving (tackling solved and/or unsolved problems, as you like). To facilitate collaboration, we'll be using a new open-source software platform called Coauthor.
Class projects more generally can take the form of folding-inspired sculptures; formulations of clean, new open problems; implementations of existing algorithms; or well-written descriptions of one or more papers in the area. Projects can be purely mathematical (geometric) and/or theoretical computer science (algorithmic/complexity theoretic) and/or artistic. Students are also required to do a project presentation and a small number of problem sets.
Additional recommended reading is Origami Design Secrets: Mathematical Methods for an Ancient Art by Robert Lang.
| Lecture Time: | Wednesdays at 2:30pm–5:00pm |
|---|---|
| Lecture Room: | MIT room 54-100 |
| First Lecture: | Wednesday, February 8, 2017 |
| Office Hours: | Sundays 5-6pm in 32-G5 lounge Mondays 3-4pm in 32-G632 |
| Professor: | Erik Demaine, 32-G680 |
| Co-lecturers: | Martin Demaine,
32-G582
Jason Ku, 32-G616 |
| TAs: |
Adam Hesterberg,
32-G635
Jayson Lynch, 32-G580 |
| Staff Email: | 6849-staff at csail.mit.edu |
| Units: | 3-0-9 |
| Prerequisites: | 6.046 or equivalent background in discrete mathematics and algorithms
Alternatively, permission from the instructor. |
| Credit: | H-level and EC-level credit; no ED credit |
| Requirements: | Participation in class, measured as posting or being @mentioned in at least one Coauthor post each week. Project write-up and presentation. Problem sets roughly weekly. |
If you are interested in attending the class, for credit or as a listener, please do the following: