Handwritten notes, page 1/8 •
[previous page] •
[next page] •
[PDF]
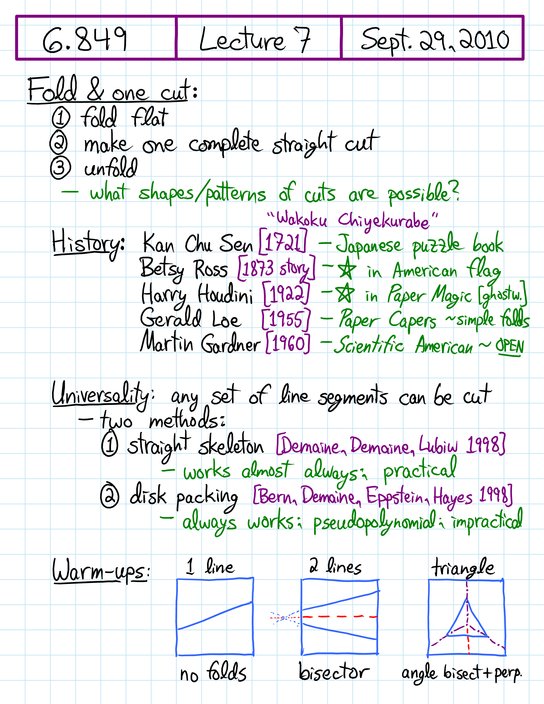
Handwritten notes, page 1/8 • [previous page] • [next page] • [PDF]
Slides, page 1/31 •
[previous page] •
[next page] •
[PDF]

“Wakoku Chiyekurabe” by Kan Chu Sen, published in 1721. Out of copyright. Scans by Erik Demaine. See http://erikdemaine.org/foldcut/sen_book.html
Slides, page 1/31 • [previous page] • [next page] • [PDF]