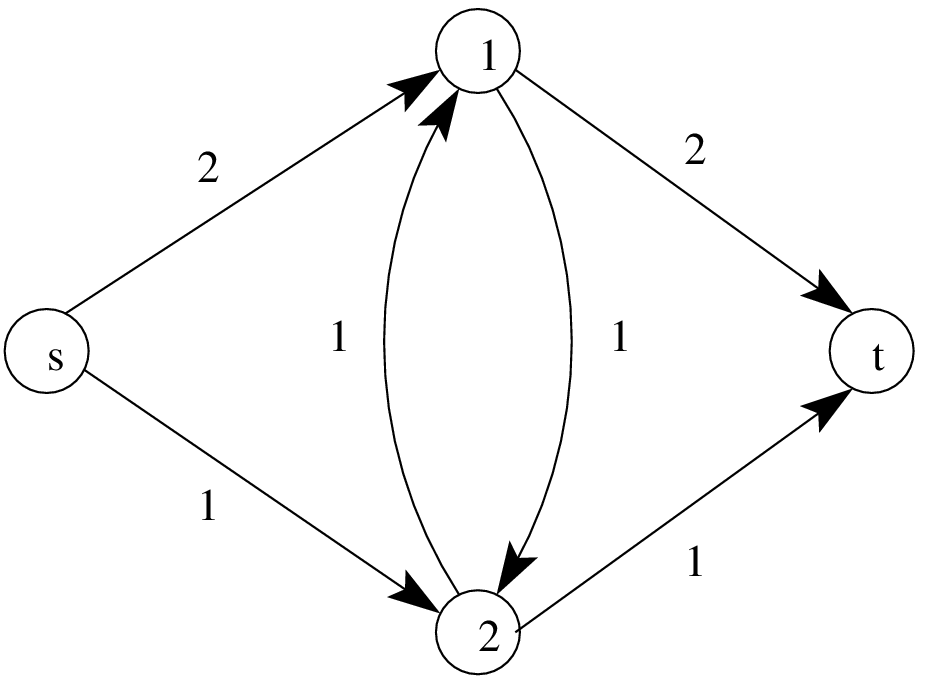
Figure 1 - An example of a network with \(n=4\) vertices and \(m=6\) edges. The capacities of the edges are shown.
\[\text{ September 24, 2003 }\] \[\text{6.854 - Advanced Algorithms}\] \[\text{Professors David Karger, Erik Demaine}\] \[\text{Alexandr Andoni, edited by Sara Mustin 9/22/06}\]
In this section we define a flow network and setup the problem we are trying to solve in this lecture: the maximum flow problem.
A network is a directed graph \(G=(V,E)\) with a source vertex \(s \in V\) and a sink vertex \(t \in V\). Each edge \(e = (v, w)\) from \(v\) to \(w\) has a defined capacity, denoted by \(u(e)\) or \(u(v, w)\). It is useful to also define capacity for any pair of vertices \((v, w) \not \in E\) with \(u(v, w) = 0\).

Figure 1 - An example of a network with \(n=4\) vertices and \(m=6\) edges. The capacities of the edges are shown.
In a network flow problem, we assign a flow to each edge. There are two ways of defining a flow: raw (or gross) flow and net flow.
Raw flow is a function \(r(v,w)\) that satisfies the following properties:
Conservation: The total flow entering \(v\) must equal the total flow leaving \(v\) for all verticles except \(s\) and \(t\).
\(\underbrace{\sum_{w\in V} r(w,v)}_{\hbox{incoming
flow}}-\underbrace{\sum_{w\in V}r(v,w)}_{\hbox{outgoing flow}}=0\), for all \(v\in
V\setminus \{s,t\}\).
Capacity constraint: The flow along any edge must be positive and less than the capacity of that edge.
\(0 \le r(v,w)\le u(v,w)\).
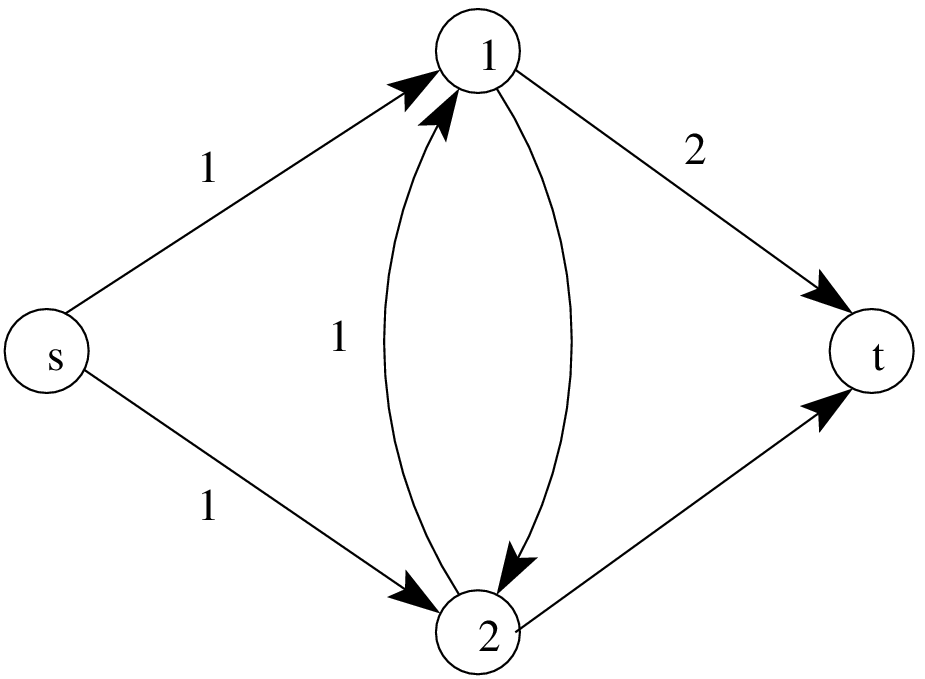
Figure 2 - An example of a raw flow for the network above. The flow has a value of 2.
With a raw flow, we can have flows going both from \(v\) to \(w\) and flow going from \(w\) to \(v\). In a net flow formulation however, we only keep track of the difference between these two flows.
Net flow is a function that satisfies the following conditions:
Skew symmetry: \(f(v,w)=-f(w,v)\).
Conservation: \(\sum_{w\in V} f(v,w)=0\), for all \(v\in V\setminus\{s,t\}\).
Capacity constraint: \(f(v,w)\le u(v,w)\) for all \(v,w\in V\).
A raw flow \(r(v, w)\) can be converted into a net flow via the formula \(f(v, w) = r(v, w) - r(w, v)\). For example, if we have 7 units of flow from \(v\) to \(w\) and 4 units of flow from \(w\) to \(v\), then the net flow from \(v\) to \(w\) is \(f(v, w) = 3\). Skew symmetry follows directly from this formula relating raw flows and net flows. Because we can convert from raw flows to net flows, for the rest of the lecture we consider only net flow problems.
Although skew symmetry relates \(f(v, w)\) and \(f(w, v)\), it is important to note that the capacity in one direction \(u(v, w)\) is independent of the capacity in the reverse direction, \(u(w, v)\).
The value of a flow is the sum of the flow on all edges leaving the source \(s\). We later show that this is equivalent to the sum of all the flow going into the sink \(t\). The value of a flow represents how much we can transport from the source to the sink. Our goal in this lecture is to solve the maximum flow problem.
The value of a flow \(f\) is defined as \(|f|=\sum_{v\in V} f(s,v)\).
Maximum flow problem: Given a network \(G = (V, E)\), find a feasible flow \(f\) with maximum value.
In this section, we show that any feasible flow can be decomposed into paths from the source to the sink and cycles. We use this fact to derive an upper bound on the maximum flow value in terms of cuts of the network.
[pathDecomp] Flow decomposition: We can decompose any feasible flow \(f\) on a network \(G\) into at most \(m\) cycles and s-t paths.
The following algorithm extracts the \(m\) paths and cycles.
Find a path with positive flow from the node \(s\) to node \(t\). (If the flow is non-zero, there exists at least one such path.)
Anti-augment the flow on this path-that is, reduce the flow in the path until the flow on some edge becomes 0.
Add this path as an element of the flow decomposition.
Continue these operations until there are no more paths from \(s\) to \(t\) with positive flow.
If there are still some edges with non-zero flow, the remaining flow can be decomposed into cycles. Find a cycle in the following way: take any edge with non-zero flow and follow an outgoing edge with non-zero flow until a cycle is found.
Anti-augment on the cycle found.
Add the cycle as an element of the flow decomposition.
Continue finding cycles until there are no more edges with non-zero flow.
Each time we anti-augment a path or a cycle, we zero out the flow on some edge. There are at most \(m\) anti-augmentations, and, consequently, \(m\) paths/cycles in the flow decomposition.
In a network flow problem, it is useful to work with a cut of the graph, particularly an s-t cut.
An s-t cut of network \(G\) is a partition of the vertices \(V\) into 2 groups: \(S\) and \(\bar{S}=V\setminus S\) such that \(s\in S\) and \(t\in \bar{S}\).
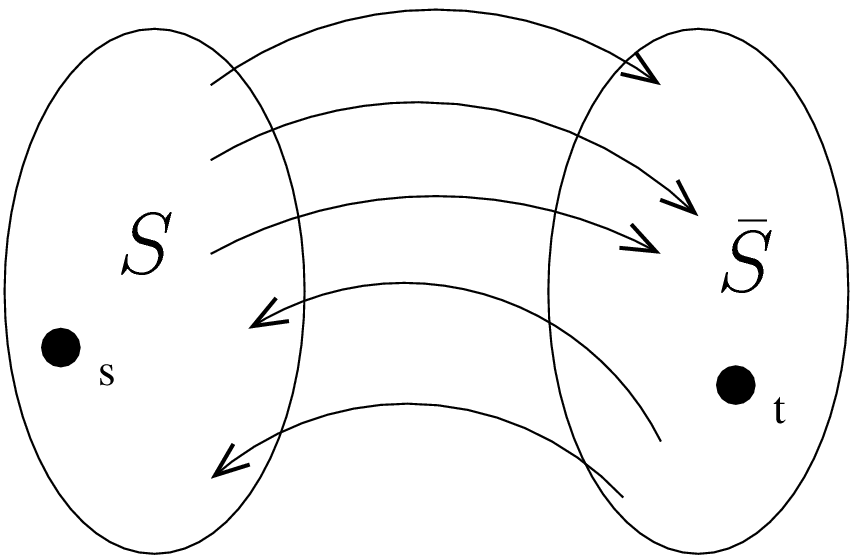
Figure 3 - An illustration of an s-t cut. There might be both edges from \(S\) to \(\bar{S}\) and from \(\bar{S}\) to \(S\).
We will usually represent a cut as the pair \((S, \bar{S})\), or just \(S\). We generalize the concept of the net flow and the capacity of an edge to define the net flow and capacity of a cut.
The net flow along cut \((S, \bar{S})\) is defined as \(f(S)=\sum_{v\in S}\sum_{w\in \bar{S}} f(v,w)\).
The value (or capacity) of a cut is defined as \(u(S)=\sum_{v\in S}\sum_{w\in \bar{S}} u(v,w)\).
In summary, the value (or capacity) of a cut is the sum of all values (capacities) of edges that go from \(S\) to \(\bar{S}\). Note that direction is important in these definitions. Capacity along an edge in the reverse direction, from \(w \in \bar{S}\) to \(v \in S\), does not count.
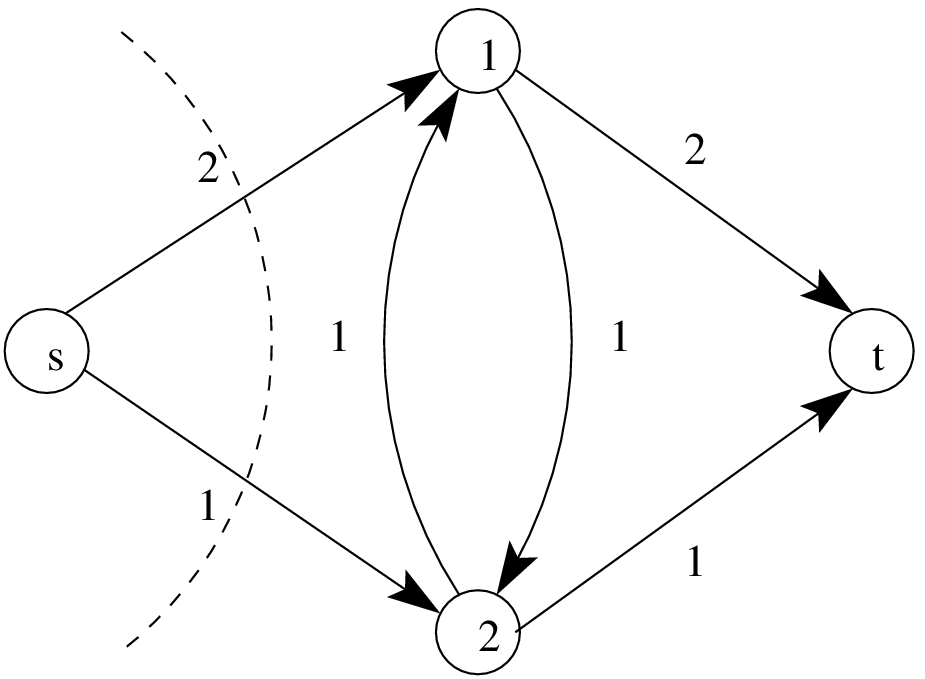
Figure 4 - An example of a cut in a network. The s-t cut is represented by a dashed line. The value (capacity) of the cut is equal to 3. This is one of the minimum s-t cuts.
Working with cuts is useful because of the following lemma: [allSTCutsSame] Given a flow \(f\), for any cut \(S\), \(f(S) = |f|\). In other words, all s-t cuts carry the same flow: the value of the flow \(f\).
We can use Lemma [pathDecomp] to prove this statement directly. We decompose the flow into s-t paths and cycles. Each s-t path must end up in \(\bar{S}\), so it must go from set \(S\) to \(\bar{S}\) one more time than it goes from \(\bar{S}\) to \(S\). Therefore, an s-t path carring \(x\) flow along that path contributes exactly \(x\) to the value of the cut. A cycle must go from \(S\) to \(\bar{S}\) the same number of times as it goes from \(\bar{S}\) to \(S\), contributing 0 to the value of the cut. Therefore the total value of the cut \(S\) is equal to the sum of the flows along every s-t path, which is equal to \(|f|\).
Alternatively, we can prove the lemma by induction on the size of the sets \(S\). For \(S={s}\), the claim is true. Now, suppose we move one vertex \(v\) from \(\bar{S}\) to \(S\). The value \(f(S)\) changes in the following way:
\(f(S)\) increases by \(f(v,\bar{S})\).
\(f(S)\) decreases by \(f(S,v) = -f(v,S)\).
In conclusion, the total change in the value of \(f(S)\) after moving the vertex \(v\) from \(S\) to \(\bar{S}\) is equal to \(f(v,\bar{S})+f(v,S)=f(v,V)=0\) (by conservation of flow).
For a flow network, we define a minimum cut to be a cut of the graph with minimum capacity. Then, Lemma [flowUpperBound] gives us an upper bound on the value of any flow.
[flowUpperBound] If \(f\) is a feasible flow, then \(|f| \le u(S)\) for any cut \(S\).
For all edges \(e\), \(f(e) \le u(e)\), so \(f(S) \le u(S)\) (the flow across any cut \(S\) is not more than the capacity of the cut). By Lemma [allSTCutsSame], \(|f| = f(S)\), so \(|f| \le u(S)\) for any cut \(S\).
If we pick \(S\) to be a minimum cut, then we get an upper bound on the maximum flow value.
In this section, we show that the upper bound on the maximum flow given by Lemma [flowUpperBound] is exact. This is the max-flow min-cut theorem.
To prove the theorem, we introduce the concepts of a residual network and an augmenting path.
Let \(f\) be a feasible flow on a network \(G\). The corresponding residual network, denoted \(G_f\), is a network that has the same vertices as the network \(G\), but has edges with capacities \(u_f(v, w) = u(v, w) - f(v, w)\). Only edges with non-zero capacity, \(u_f(v,w)>0\), are included in \(G_f\).
Note that the feasibility conditions imply that \(u_f(v,w)\ge 0\) and \(u_f(v,w)\le u(v,w)+u(w,v)\). This means all capacities in the residual network will be non-negative.
An augmenting path is a directed path from the node \(s\) to node \(t\) in the residual network \(G_f\).
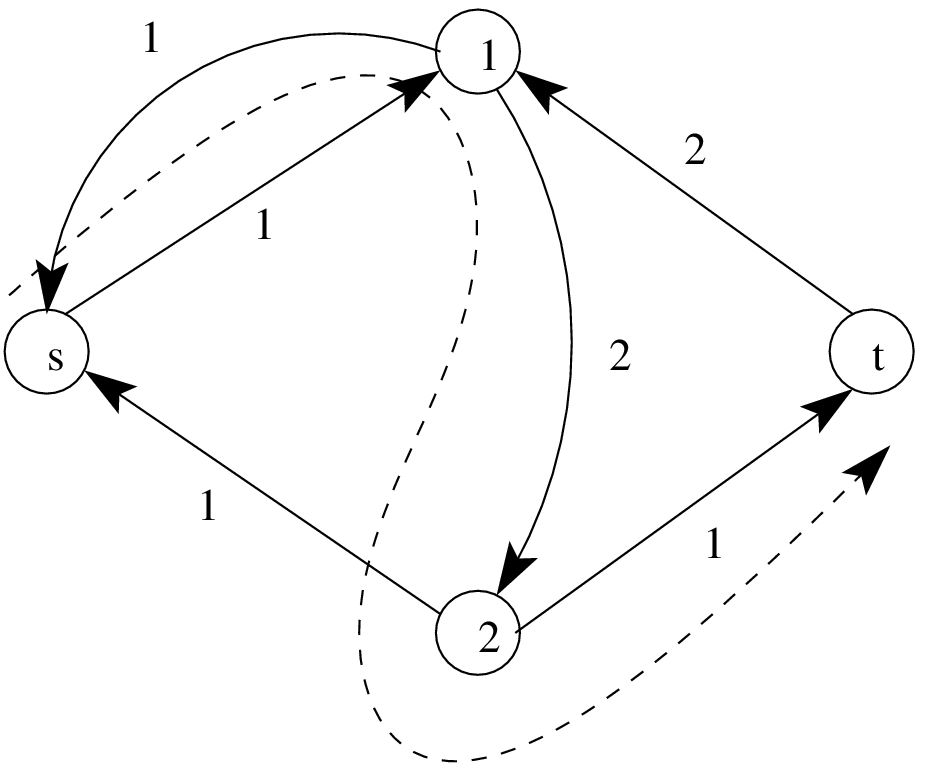
Figure 5 - An example of a residual network. This residual network corresponds to the network depicted in Figure 1 and the flow in Figure 2. The dashed line corresponds to a possible augmenting path.
Note that if we have an augmenting path in \(G_f\), then this means we can push more flow along such a path in the original network \(G\). To be more precise, if we have an augmenting path \((s, v_1, v_2, \dots v_k, t)\), the maximum flow we can push along that path is \(\min\{u_f(s, v_1), u_f(v_1, v_2), u_f(v_2, v_3), \dots u_f(v_{k-1}, v_k), u_f(v_{k}, t)\}\). Therefore, for a given network \(G\) and flow \(f\), if there exists an augmenting path in \(G_f\), then the flow \(f\) is not a maximum flow.
More generally, if \(f'\) is a feasible flow in \(G_f\), then \(f + f'\) is a feasible flow in \(G\). The flow \(f + f'\) still satisfies conservation because flow conservation is linear. The flow \(f + f'\) is feasible because we can rearrange the inequality \(f'(e) \le u_f(e) = u(e) - f(e)\) to get \(f'(e) + f(e) \le u(e)\). Conversely, if \(f'\) is a feasible flow in \(G\), then the flow \(f - f'\) is a feasible in \(G_f\).
Using residual networks and augmenting paths, we can state and prove the max-flow min-cut theorem.
(Max-flow min-cut theorem). In a flow network \(G\), the following conditions are equivalent:
A flow \(f\) is a maximum flow.
The residual network \(G_f\) has no augmenting paths.
\(|f| = u(S)\) for some cut \(S\).
These conditions imply that the value of the maximum flow is equal to the value of the minimum s-t cut: \(\max_f |f|=\min_S u(S)\), where \(f\) is a flow and \(S\) is a s-t cut.
We show that each condition implies the other two.
\(1 \Rightarrow 2\): If there is an augmenting path in \(G_f\), then we previously argued that we can push additional flow along that path, so \(f\) was not a maximum flow. \(1 \Rightarrow 2\) is the contrapositive of this statement.
\(2 \Rightarrow 3\):
If the residual network \(G_f\) has no augmenting paths, \(s\) and \(t\) must be disconnected. Let \(S=\{\)vertices reachable from \(s\) in \(G_f \}\). Since \(t\) is not reachable, the set \(S\) describes a s-t cut.
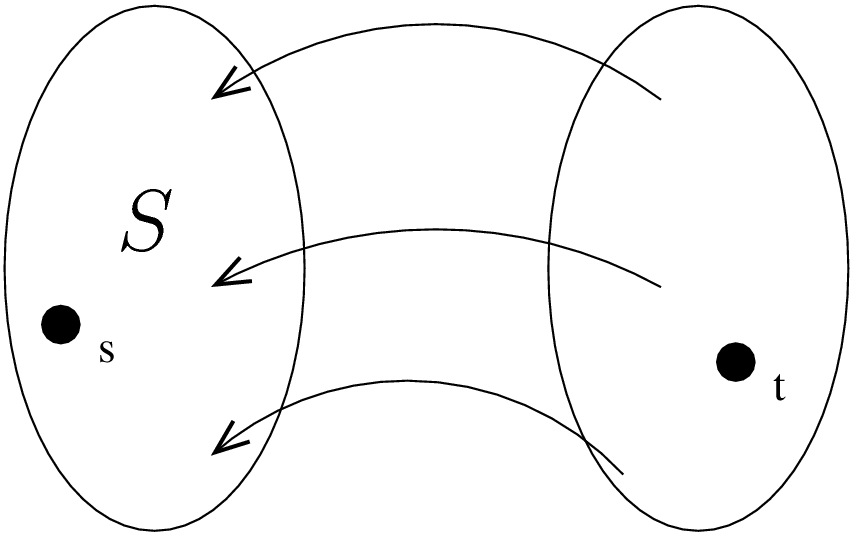
Figure 5 - Network \(G_f\) is disconnected. The set \(S\) contains all the nodes that are reachable from \(s\).
By construction, all edges \((v,w)\) crossing the cut have residual capacity 0. This means in the original network \(G\), these edges have \(f(v,w)=u(v,w)\). Therefore, \(|f|=f(S)=u(S)\).
\(3 \Rightarrow 1\): If for some cut \(S\), \(|f| = u(S)\), we know \(f\) must be a maximum flow. Otherwise, we would have a flow \(g\) with \(|g| > u(S)\), contradicting Lemma [flowUpperBound].
From (1) and (3), we know that the maximum flow cannot be less than the value of the minimum cut, because for some \(S\), \(|f| = u(S)\) and \(u(S)\) is at least as big as the minimum cut value. Lemma [flowUpperBound] tells us that the maximum flow can not be greater than the minimum cut value. Therefore, the maximum flow value and the minimum cut value are the same.
The Ford-Fulkerson algorithm solves the problem of finding a maximum flow for a given network. The description of the algorithm is as follows:
Start with \(f(v,w) = 0\).
Find an augmenting path from \(s\) to \(t\) in \(G_f\) (using, for example, a depth first search or similar algorithms).
Use the augmenting path found in the previous step to increase the flow.
Repeat until there are no more augmenting paths in \(G_f\).
If the capacities are all integers, then the running time is \(O(m|f|)\). This is true because finding an augmenting path and updating the flow takes \(O(m)\) time, and every augmenting path we find must increase the flow by an integer that is at least 1.
In general, if we have integral capacities, then our solution satisfies an integrality property: there exists an integral maximal flow. This happens because every augmenting path increases flows by an integer amount.
Since the running time is directly proportional to the value of the maximal flow, this particular algorithm is only good for cases when the value \(|f|\) is small. For example, when all capacities are at most 1, the maximum flow \(|f|\) is at most \(n\). In general, the algorithm may be as bad as linear in unary representation of the input. Figure [fig:exbadFF] illustrates a bad case for this form of the Ford-Fulkerson algorithm.
We describe such an algorithm as being pseudo-polynomial, because it is polynomial in terms of variables we care about (but not necessarily the input).
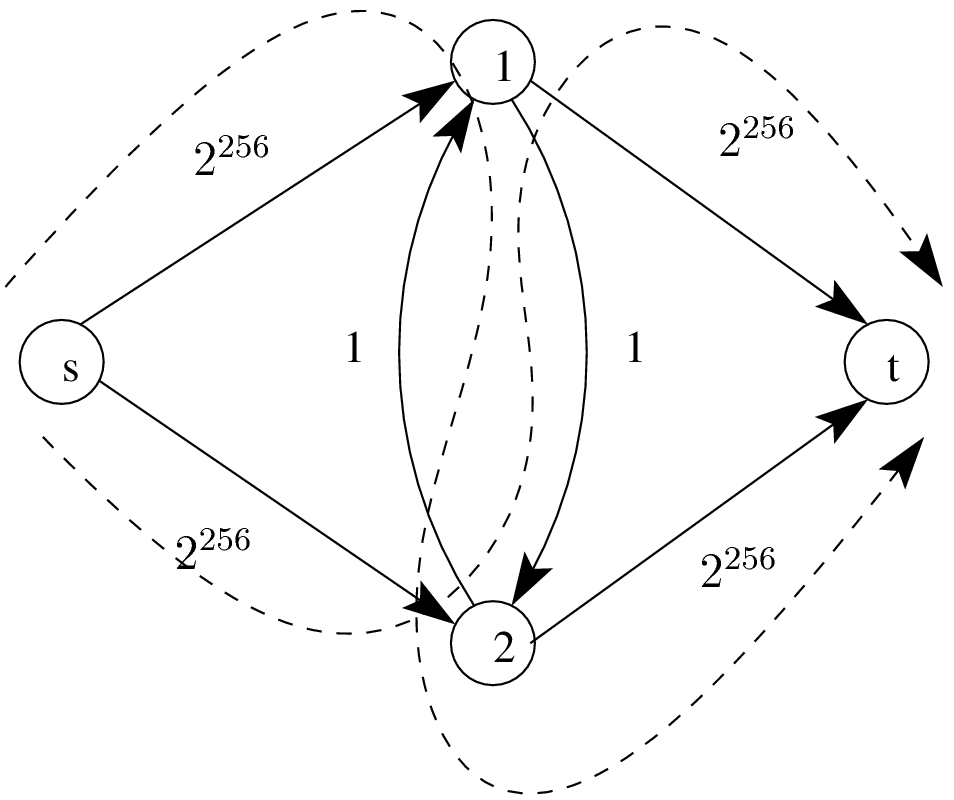
Figure 6 - An example for which the Ford-Fulkerson, in the stated form, might perform very badly. The algorithm runs slowly if at each step, the augmentation path is either \(s\rightarrow 1 \rightarrow 2 \rightarrow t\) or \(s \rightarrow 2 \rightarrow 1 \rightarrow t\) (shown with dashed lines). At an augmentation, the flow will increase by at most \(2\).
If the capacities are rational, then it can be shown that the algorithm will finish. It might, however, require more than \(O(m|f|)\) time. If the capacities are real, the algorithm might never finish, or even converge to a non-optimal value.
If we setup better rules for selecting the augmentation paths however, we might get better results. Before showing some improvements to the Ford-Fulkerson algorithm, we will introduce some new notions on the running time of algorithms.
An algorithm is psuedo-polynomial if it is polynomial in the unary representation of the input.
An algorithm is weakly polynomial if it is polynomial in the binary representation of the input.
An algorithm is strongly polynomial if it is polynomial in combinatorial complexity of input. (For example, in the case of max-flow problem, the algorithm would have to be polynomial in \(n\) and \(m\).)
The are at least two possible ideas for improving the Ford-Fulkerson algorithm. Both of the improvements rely on a better choice of an augmenting path (rather than a random selection of an augmenting path).
Using breadth-first search, we can choose shortest-length augmenting path. With this path-selection rule, the number of augmentations is bounded by \(n\cdot m\), and thus the running time of the algorithm goes down to \(O(nm^2)\) time.
We can also choose the maximum-capacity augmenting path: the augmenting path among all augmenting paths that increases the flow the most (max-capacity augmenting path). It is possible to find such a path in \(O(m\log n)\) time using a modified Dijkstra's algorithm (ignoring the cycles). The number of augmentations will be at most \(m\ln|f|\le m\ln(nU)\), where \(U=\max\{u(v,w)\}\) (for integral capacities).
In this lecture we prove the time bound for the second improvement. Consider the maximum flow \(f\) in the current residual network. We apply the flow-decomposition lemma, Lemma [pathDecomp] (discarding the cycles because they do not modify \(|f|\)). There are at most \(m\) paths carrying all the flow, so there must be at least one path carrying at least \(\frac{|f|}{m}\) flow. Therefore, the augmenting path with maximum capacity increases the flow in the original network by at least \(\frac{|f|}{m}\). This decreases the maximum possible flow in the residual graph from \(|f|\) to \((1-\frac{1}{m})|f|\) (remember, the smaller is the maximum possible flow in the residual graph, the greater is the corresponding flow in the original graph).
We need to decrease the flow \(|f|\) by a factor of \((1-\frac{1}{m})\) about \(m\ln|f|\) times before we decrease the max flow in the residual graph to 1. This is because
\[|f| \left(1-\frac{1}{m}\right)^{m\ln |f|}\approx |f| \left(\frac{1}{e}\right)^{\ln |f|}\approx 1.\]
In one more step, the residual graph will have a maximum flow of 0, meaning that the corresponding flow in the original graph is maximal. Thus, we need \(O(m\ln |f|)\) augmentations. Since one augmentation step takes about \(O(m\log n)\) time, the total running time is \(O(m^2 \ln|f| \cdot \ln n)\). This algorithm is weakly polynomial, but not strongly polynomial.
We can also improve the running time of the Ford-Fulkerson algorithm by using a scaling algorithm. The idea is to reduce our max flow problem to the simple case, where all edge capacities are either 0 or 1.
The scaling idea, described by Gabow in 1985 and also by Dinic in 1973, is as follows:
Scale the problem down somehow by rounding off lower order bits.
Solve the rounded problem.
Scale the problem back up, add back the bits we rounded off, and fix any errors in our solution.
In the specific case of the maximum flow problem, the algorithm is:
Start with all capacities in the graph at 0.
Shift in the higher-order bit of each capacity. Each capacity is then either 0 or 1.
Solve this maximum flow problem.
Repeat this process until we have processed all remaining bits.
This description of the algorithm tells us how to scale down the problem. However, we also need to describe how to scale our algorithm back up and fix the errors.
To scale back up:
Start with some max flow for the scaled-down problem. Shift the bit of each capacity by 1, doubling all the capacities. If we then double all our flow values, we still have a maximum flow.
Increment some of the capacities. This restores the lower order bits that we truncated. Find augmenting paths in the residual network to re-maximize the flow.
We will need to find at most \(m\) augmenting paths. Before we scaled our problem back up, we had solved a maximum flow problem, so some cut in the residual network had 0 capacity. Doubling all the capacities and flows keeps this the same. When we increment the edges however, we increase the cut capacity by at most \(m\): once for each edge. Each augmenting path we find increases the flow by at least 1, so we need at most \(m\) augmenting paths.
Each augmenting path takes at most \(O(m)\) time to find, so we spend \(O(m^2)\) time in each iteration of the scaling algorithm. If the capacity of any edge is at most \(U\), which is an \(O(\lg U)\) bit number, we require \(O(\lg U)\) iterations of the scaling algorithm.
Therefore the total running time of the algorithm is \(O(m^2 \lg U)\). This algorithm is also a weakly polynomial algorithm.