| [+] Fold and one cut: history, straight-skeleton method, disk-packing method, simple folds, higher dimensions, flattening polyhedra. | ||||
| This lecture is about my first work in computational origami: folding a piece of paper flat so that one complete straight cut makes a desired pattern of cuts (and resulting polygonal shapes). The problem has a long history (back to the 1700s) and possible applications to airbag folding through a problem called flattening. We'll see two different methods for this problem, each with connections to the tree method of origami design: the first generalizes the universal molecule to nonconvex polygons, but loses the ability to control the shadow tree; the second uses disk packing (but no rivers) and universal molecules for triangles and quadrangles. I'll also talk about a brand new result that started from this class three years ago: what shapes can you make only with simple folds? | ||||
|
Handwritten notes, page 1/8 •
[previous page] •
[next page] •
[PDF]
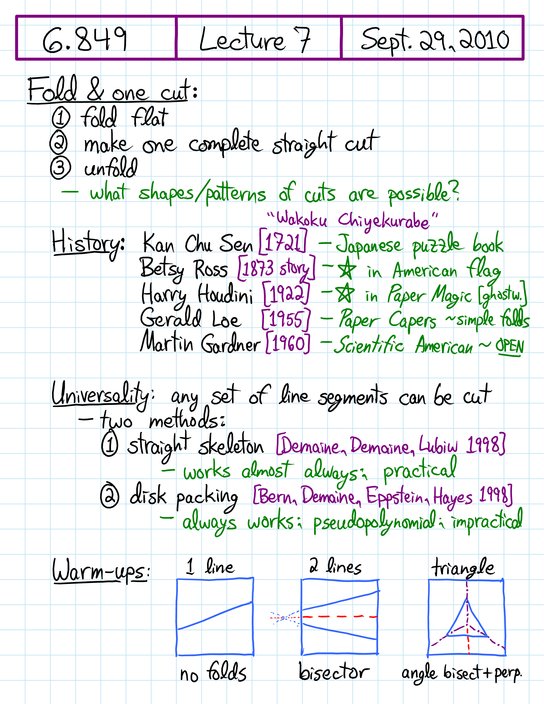
Handwritten notes, page 1/8 • [previous page] • [next page] • [PDF] |
|
|
Slides, page 1/31 •
[previous page] •
[next page] •
[PDF]
“Wakoku Chiyekurabe” by Kan Chu Sen, published in 1721. Out of copyright. Scans by Erik Demaine. See http://erikdemaine.org/foldcut/sen_book.html Slides, page 1/31 • [previous page] • [next page] • [PDF] |
The video above should play if your web browser supports either modern Flash or HTML5 video with H.264 or WebM codec. The handwritten notes and slides should advance automatically. If you have any trouble with playback, email Erik.
