Homework 0: Buffon-Laplace Needle Problem

DUE DATE EXTENDED TO 2/24 (11:59PM)

Notes:

Don't attempt to use mm or mo to parallelize your Star-P code. Instead, construct a distributed random matrix and conduct tests for inside/outside in parallel (a *very* small modification of the serial version).
Don't use more than 4 threads with your OpenMP code. (Any more will result in multiple threads on a single processor, which you don't want.) Similarly, don't use more than 64 processes with your MPI code.
Don't worry about slow behavior in OpenMP when using multiple threads.

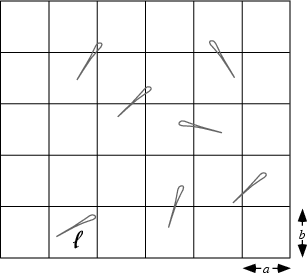
Imagine that a needle of length l is dropped onto a floor with a grid of equally spaced parallel lines distances a and b apart, where l is less then a and b. The probabilty that the needle will land on at least one line is given by

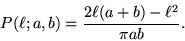
( Refer to Mathworld for more details ) Thus, by running a Monte-Carlo simulation of needle drops, we can estimate pi.

How to submit

mkdir hw0
copy all relevant code (e.g. source, write-ups, plots into hw0)
tar cf `whoami`-hw0.tar hw0/
gzip `whoami`-hw0.tar
cp `whoami`-hw0.tar.gz ~
It'll be collected by a cron job

All the files you need for this problem set are contained here.

Question 0

We have given you serial versions of the Buffon-Laplace Needle simulation, one in MATLAB and one in C. The MATLAB version first generates a pile of random numbers, interprets them as parameters in a Buffon simulation, counts up the intersections and returns the appropriate fraction. The serial programs are based on exploiting a particular symmetry in the problem. They only consider a single box and randomly generate perpendicular distances and the needle tilt. (In so doing, they use the build in value of pi; we know this is circular, and there are ways around this, but accurate computation of pi isn't actually the focus of the problem.) Your fist job is to understand these example programs (or produce your own). Remember to link the serial programs with -lm before running them.

Question 1

Your second job is to produce 3 parallel programs for computing pi via the Buffon approach, one using MPI, one using STAR-P and one using OpenMP. We have provided skeleton files for the MPI and OpenMP versions which accept the required command-line arguments (a, b, l, numTrials, outputfilename) and which log their output to outputfilename in the required format. Use them if you like, or roll your own. These skeletons are in BuffonFoo.skeleton.c where Foo is either MPI or OpenMP. We have also provided makefiles which will correctly compile your programs (assuming your parallel sources are BuffonMPI.c and BuffonOpenMP.c). Use these makefiles via

make -f Makefile.MPI
make -f Makefile.OpenMP

The source for the MPI and OpenMP versions will be a simple combination of the serial source, the skeleton file, and a few parallel directives. Nothing fancy is needed. However, MAKE SURE YOU SEED THE RANDOM NUMBER GENERATORS DIFFERENTLY ON EACH PROCESSOR in MPI. An easy way to do this is to combine both the current time and the node's rank in your srand call. Test your OpenMP and MPI code on a=1.0, b=1.0, l=0.5, numTrials=1e6 with 4 processors. Make sure the output names provided are mpi-test and openmp-test. OpenMP will default to 4 processors; to run the program, ssh to a free node (found via jmon) then do:

export LD_LIBRARY_PATH=/opt/intel_cc_80/lib
./BuffonOpenMP.exe 1.0 1.0 0.5 1000000 openmp-test

To run the MPI version, do:

lamboot; mpirun -np 4 ./BuffonMPI.exe 1.0 1.0 0.5 1000000 mpi-test

The output from the runs will be stored in openmp-test.out and mpi-test.out respectively. Test your STAR-P version under the same conditions. Save your STAR-P function in a file BuffonSTARP.m. To run the STAR-P version, do:

startmp 4

Then within MATLAB, call the function you wrote. It is also straightforward to parallelize. Enclose the function in the matlab directives tic and toc to get timing information.

Question 2

Produce plots showing how your STAR-P and MPI versions scale as more processors are added. Try each on 1e3 needles with 2, 4 and 8 processors, as well as 1e7 needles with 2, 4, 8 and 16 processors. Include the STAR-P output however you wish. Make sure the outputs from the MPI runs are named mpi-(large/small)-(num procs).out. Large refers to 1e7 needles and small to 1e3. For example, to run the MPI test with 1e7 needles on 8 processors, you'd do:

lamboot; mpirun -np 8 ./BuffonMPI.exe 1.0 1.0 0.5 10000000 mpi-large-8

Clearly explain any differences in scalability that you observe. Include both your plots and your verbal explanations in a file writeup.pdf or writeup.ps in your submission.

The pictures above is taken from:

Weisstein, Eric W. "Buffon-Laplace Needle Problem" 
Eric Weisstein's World of Mathematics. 
http://mathworld.wolfram.com/Buffon-LaplaceNeedleProblem.html