Sparse Matrix Representation

The sparse matrix K is represented in the compressed-column format, which is defined as follows. Let nnz be the number of nonzero elements in the matrix, and let n be the number of columns. The matrix is then represented by the following three arrays:

Pr

- Double precision vector with nnz elements. Contains the values of each matrix entry, in column-wise order starting with the lowest column.

Ir

- Integer vector with nnz elements. Contains the row indices for each matrix entry.

Jc

- Integer vector with n+1 elements. The ith element is an integer specifying the index of the first element in the ith column. Note that element n+1 is nnz.

The following operations on sparse matrices are implemented:

Creating the matrix.

The matrix is created by first counting all the elements in each column. Next, the elements are inserted and sorted within each column. After this, all duplicate elements can be removed, and finally the three arrays according to above can be formed.

Setting the value of a matrix element.

Since the elements in each column are sorted, the position of an element can be extracted using a binary search within the column. The time for this is about the logarithm of the number of elements in the column, which is bounded independently of the size of the mesh.

Multiplying matrix by vector.

This is straightforward, by noting the following way to write a matrix-vector product:

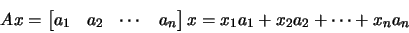$$Ax= \begin{bmatrix} a_1 & a_2 & \cdots & a_n \end{bmatrix}x = x_1a_1+x_2a_2+\cdots+x_na_n$$ (5)

In words, each column is multiplied by an element of x and added to the result. The compress-column format is well suited for this operation.