6.889: Algorithms for Planar Graphs and Beyond (Fall 2011)

Erik Demaine, Shay Mozes, Christian Sommer, Siamak Tazari

[Home] [Problem Sets] [Project] [Lectures] [Problem Session Notes] [Klein's Book] [Accessibility]

Lecture 5 Video     [previous] [next]

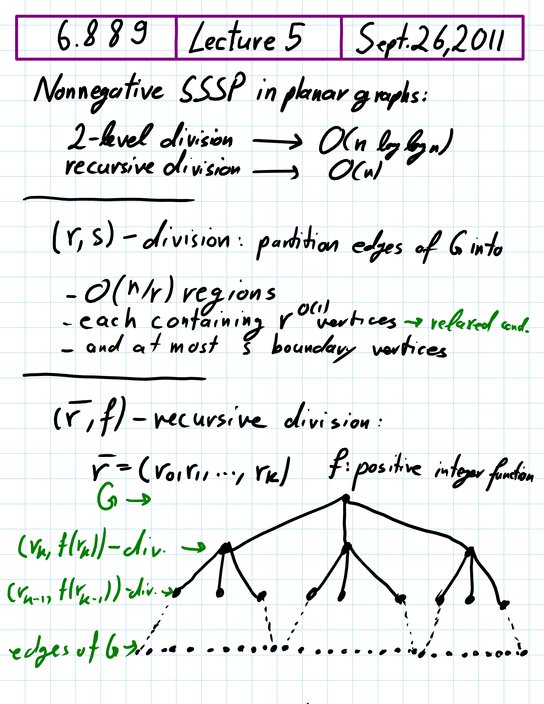
[+] Shortest paths and recursive divisions in minor-free graphs.

We discuss recursive divisions and how to obtain them in planar and minor-free graphs. This is one of the main tools that is used to obtain a linear-time SSSP algorithm and, in fact, once we have a suitable recursive division, the same SSSP algorithm works for both planar and minor-closed classes. However, both the recursive division algorithm and the SSSP analysis require the graph to be of bounded degree and it turns out that, in general H-minor-free graphs, a reduction to the bounded-degree case as in the planar case is not possible. We will see how to use knitted H-partitions to overcome this issue and obtain a generalized recursive division algorithm for all H-minor-free classes.

[HKRS97] M. R. Henzinger, P. N. Klein, S. Rao, S. Subramanian: Faster shortest path algorithms for planar graphs. In: Journal of Computer and System Sciences, vol. 55(1):pp. 3-23, 1997.
[RW09] B. Reed, D. R. Wood: A linear-time algorithm to find a separator in a graph excluding a minor. In: ACM Transactions on Algorithms, vol. 5(4):pp. 1-16, 2009.
[TM09] S. Tazari, M. Müller-Hannemann: Shortest paths in linear time on minor-closed graph classes, with an application to Steiner tree approximation. In: Discrete Applied Mathematics, vol. 157:pp. 673-684, 2009.
[Taz10, Chapter 5] S. Tazari: Algorithmic Graph Minor Theory: Approximation, Parameterized Complexity, and Practical Aspects. Doctoral Dissertation, Humboldt-Universität zu Berlin, 2010.

Download Video: 360p, 720p

Lecture notes, page 1/9 • [previous page] • [next page] • [PDF]

Lecture notes, page 1/9 • [previous page] • [next page] • [PDF]

The video above should play if your web browser supports either modern Flash or HTML5 video with H.264 or WebM codec. The lecture notes should advance automatically. If you have any trouble with playback, email Erik.