[+]
Pleat folding: “Hyperbolic paraboloid”,
circular pleat, self-folding origami,
plastic deformation and elastic memory;
triangulation, interval arithmetic; how paper folds between
creases, ruled surfaces, torsal, straight creases stay straight,
polygons stay flat; nonexistence.
|
|
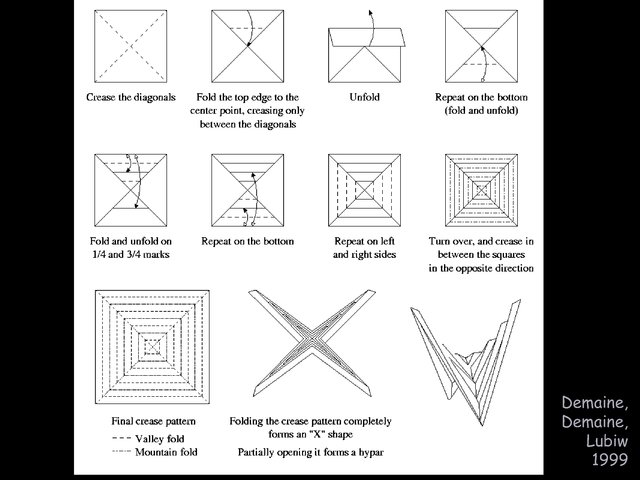
This lecture is primarily about pleat folding, specifically
the so-called “hyperbolic paraboloid” model common in origami
and originating at the Bauhaus in the late 1920s. Surprisingly,
this origami model does not exist: it's impossible to fold anything
nonflat with a crease pattern consisting of concentric squares and
diagonals. We'll prove this, using a new theory for how paper folds
in between creases, in particular showing that straight creases stay
straight when folded, and interior polygons stay flat when folded.
By contrast, we'll show how the “hyperbolic paraboloid” folds fine
after adding specific diagonal creases to the trapezoidal faces.
Afterward, we'll briefly look at a couple of related topics: how to maximally inflate a teabag or other polyhedral surface by folding, and what kind of foldings are possible with curved creases. On the latter topic, I'll overview a big ongoing project in which we're trying to reconstruct the mathematics underlying a beautiful series of sculptures folded by David Huffman from the 1970s–1990s. |
|
Handwritten notes, page 1/9 •
[previous page] •
[next page] •
[PDF]
Handwritten notes, page 1/9 • [previous page] • [next page] • [PDF] |
|
|
Slides, page 1/38 •
[previous page] •
[next page] •
[PDF]
Figure by the authors. See http://erikdemaine.org/hypar/ Slides, page 1/38 • [previous page] • [next page] • [PDF] |
The video above should play if your web browser supports either modern Flash or HTML5 video with H.264 or WebM codec. The handwritten notes and slides should advance automatically. If you have any trouble with playback, email Erik.
