6.849: Geometric Folding Algorithms: Linkages, Origami, Polyhedra (Fall 2010)

Prof. Erik Demaine

[Home] [Problem Sets] [Project] [Lectures] [Problem Session Notes] [Accessibility]

Lecture 17 Video     [previous] [next]

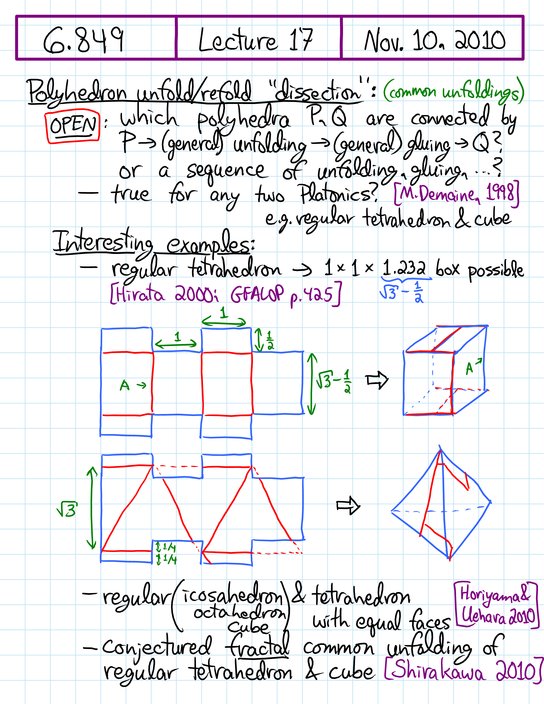
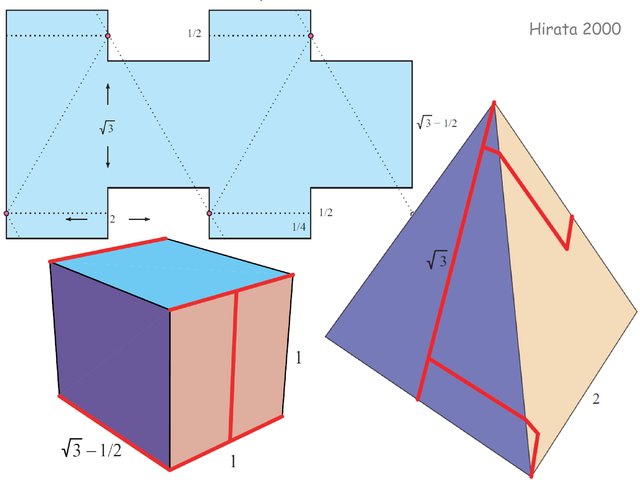
[+] Polyhedron refolding: Dissection-like open problem, regular tetrahedron to box, Platonic solids to tetrahedra, box to box, polycubes, orthogonal unfoldings with nonorthogonal foldings.
Smooth polyhedron folding: Smooth Alexandrov, D-forms, ribbon curves.
Smooth polyhedron unfolding: Smooth prismatoids.
Smooth origami: wrapping smooth surfaces with flat paper, Mozartkugel, contractive mapping, Burago-Zalgaller Theorem (crinkling/crumpling), stretched path, stretched wrapping, source wrapping, strip wrapping, petal wrapping, comb wrapping, Pareto curve.

This lecture is a big collection of fun results related to unfolding, refolding, and smooth folding:
  • common unfolding of a regular tetrahedron and near-cube
  • common unfoldings of Platonic solids and near-regular tetrahedra
  • common unfoldings of boxes of different sizes
  • common unfoldings of many polycubes
  • orthogonal unfoldings with nonorthgonal foldings
  • smooth Alexandrov's theorem, applied to smooth convex shapes (D-forms)
  • unfolding smooth convex polyhedra (prismatoids)
  • wrapping (paper folding) smooth surfaces like spheres, using a new definition of origami, where distances can shrink instead of necessarily staying the same
The last section has practical applications to computational confectionery, reducing the material usage in wrappings of spherical chocolates such as Mozartkugel. Yum!

Download Video: 360p, 720p

Handwritten notes, page 1/11 • [previous page] • [next page] • [PDF]

Handwritten notes, page 1/11 • [previous page] • [next page] • [PDF]

Slides, page 1/24 • [previous page] • [next page] • [PDF]

Figures 25.51 & 25.52 of GFALOP

Slides, page 1/24 • [previous page] • [next page] • [PDF]

The video above should play if your web browser supports either modern Flash or HTML5 video with H.264 or WebM codec. The handwritten notes and slides should advance automatically. If you have any trouble with playback, email Erik.